Fréquence de quadrature et démodulation de phase

Démodulation radiofréquence

Cette page explore l'utilisation de la démodulation en quadrature avec des signaux modulés en fréquence et en phase.

De la page précédente, nous savons que la démodulation en quadrature produit deux formes d'onde en bande de base qui, prises ensemble, transmettent les informations qui ont été codées dans la porteuse du signal reçu. 

Plus précisément, ces formes d'onde I et Q sont équivalentes aux parties réelles et imaginaires d'un nombre complexe. 

La forme d'onde en bande de base contenue dans le signal modulé correspond à une représentation en amplitude plus phase des données originales, et la démodulation en quadrature convertit cette représentation en amplitude plus phase en signaux I et Q qui correspondent à une représentation cartésienne.

Il n'est peut-être pas très surprenant que nous puissions utiliser la démodulation en quadrature pour démoduler les signaux AM, étant donné qu'un démodulateur en quadrature est simplement deux démodulateurs d'amplitude entraînés par des signaux de référence de fréquence porteuse qui ont une différence de phase de 90 °.

 Cependant, l'une des caractéristiques les plus importantes de la démodulation en quadrature est son universalité. Il fonctionne non seulement avec la modulation d'amplitude mais également avec la modulation de fréquence et de phase.

Démodulation de fréquence en quadrature
Examinons d'abord les formes d'onde I et Q qui sont produites lorsque nous appliquons la démodulation en quadrature à la modulation de fréquence. La forme d'onde FM reçue est une porteuse de 100 kHz modulée par une sinusoïde de 100 Hz. 

Nous utilisons le même démodulateur en quadrature que celui utilisé dans la simulation AM; il a deux sources de tension comportementales arbitraires pour effectuer la multiplication, et chaque source de tension est suivie d'un filtre passe-bas à deux pôles (la fréquence de coupure est d'environ 1 kHz). 

Vous pouvez vous référer à la page Comment démoduler une forme d'onde FM pour plus d'informations sur la création d'un signal FM dans LTspice.

La réaction commune à ce complot serait peut-être la confusion. Qu'est-ce que ces signaux étranges ont à voir avec la sinusoïde à fréquence constante qui devrait résulter du processus de démodulation? Faisons d'abord deux observations:

* De toute évidence, la fréquence des signaux I et Q n'est pas constante. Vous pouvez trouver cela un peu déroutant au début, car nous savons que la modulation I / Q implique la modulation d'amplitude des porteuses en quadrature. Pourquoi la fréquence change-t-elle également? Il est essentiel de se rappeler que ces signaux I / Q correspondent aux signaux modulants, et non aux sinusoïdes en quadrature qui seraient additionnés dans un modulateur en quadrature. La fréquence des porteuses en quadrature modulée ne change pas, mais les formes d'onde en bande de base qui servent de signaux de modulation d'amplitude n'ont pas nécessairement une fréquence constante.

* Bien que nous ne puissions pas interpréter intuitivement les informations de ce graphique, nous pouvons voir que les signaux présentent des variations périodiques et que ces variations correspondent à la période (= 10 ms) du signal en bande de base de 100 Hz.

Trouver l'angle
Maintenant que nous avons des signaux I / Q, nous devons en quelque sorte les transformer en une forme d'onde démodulée normale. Essayons d'abord l'approche que nous avons utilisée avec la modulation d'amplitude: utilisez un peu de mathématiques pour extraire les données d'amplitude.

De toute évidence, cela n'a pas fonctionné: le signal de magnitude (la trace rouge) ne ressemble pas à une sinusoïde et la fréquence est incorrecte (200 Hz au lieu de 100 Hz). Après un examen plus approfondi, cependant, ce n'est pas surprenant. 

Les données originales sont caractérisées par l'amplitude et la phase; lorsque nous appliquons le calcul √ (I2 + Q2), nous extrayons la magnitude. Le problème est que les données originales n'étaient pas codées dans la grandeur de la porteuse - elles étaient codées dans l'angle (rappelez-vous que la modulation de fréquence et la modulation de phase sont deux formes de modulation d'angle).

Essayons donc un autre calcul. Extrayons l'angle des données I / Q plutôt que la magnitude. Comme le montre le diagramme triangulaire ci-dessus, nous pouvons le faire en appliquant l'équation suivante:

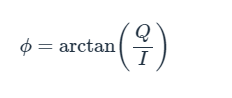
Voici le résultat:


 

Cela ne semble pas bon, mais nous approchons en fait. La trace rouge représente la phase instantanée des données d'origine. (Notez que la trace semble plus erratique qu'elle ne l'est vraiment parce que l'angle saute de –90 ° à + 90 °, ou vice versa). 

La modulation de fréquence, bien que basée sur la phase, ne code pas les informations directement dans la phase de la porteuse. Au contraire, il code des informations dans la fréquence instantanée de la porteuse, et la fréquence instantanée est la dérivée de la phase instantanée. Alors, que se passe-t-il si nous prenons la dérivée de la trace rouge?

Comme vous pouvez le voir, nous avons maintenant récupéré une forme d'onde qui est sinusoïdale et a la même fréquence que le signal de bande de base d'origine.

Comment concevoir un circuit Arctangent
À ce stade, vous vous demandez peut-être pourquoi quelqu'un voudrait s'embêter avec la démodulation I / Q. Comment diable pourrait-on concevoir un circuit qui génère un signal de sortie correspondant à la dérivée de l'arc tangente de deux signaux d'entrée? 

Eh bien, pour répondre à la question posée dans le titre de cette section, vous numérisez les signaux et calculez l'arctangente dans le firmware ou le logiciel. Et cela nous amène à un point important: la démodulation en quadrature est particulièrement avantageuse dans le contexte des radios définies par logiciel.

Une radio définie par logiciel (SDR) est un système de communication sans fil dans lequel des parties importantes de la fonctionnalité de l'émetteur et / ou du récepteur sont implémentées via un logiciel. La démodulation en quadrature est très polyvalente et permet à un seul récepteur de s'adapter presque instantanément à différents types de modulation. 

Cependant, les signaux de sortie I / Q sont beaucoup moins simples qu'un signal en bande de base normal produit par les topologies de démodulateur standard. C'est pourquoi un démodulateur en quadrature et un processeur de signal numérique forment un tel système de récepteur haute performance: le processeur de signal numérique peut facilement appliquer des opérations mathématiques compliquées aux données I / Q produites par le démodulateur.

Démodulation en phase de quadrature
Les mêmes considérations générales que nous avons discutées dans le contexte de la démodulation de fréquence en quadrature s'appliquent également à la démodulation de phase en quadrature. Cependant, pour récupérer les données d'origine, nous prenons l'arctangente de (Q / I) plutôt que la dérivée de l'arctangente de (Q / I), car le signal en bande de base est codé directement dans la phase de la porteuse plutôt que dans la dérivée de la phase (c.-à-d. la fréquence).

Le tracé suivant a été généré en appliquant une démodulation en quadrature à une forme d'onde de déphasage composée d'une porteuse de 100 kHz et d'un signal de bande de base numérique de 100 Hz qui fait changer la phase de la porteuse de 180 ° selon que le signal est logique haut ou logique faible. Comme vous pouvez le voir, la trace rouge (dont la valeur correspond à la phase de la forme d'onde reçue) reproduit les transitions logiques dans le signal de bande de base.

Notez que la trace rouge est calculée via la fonction «atan2». L'arctangente standard est limitée à deux quadrants (c.-à-d. 180 °) du plan cartésien. La fonction atan2 examine les polarités individuelles des valeurs d'entrée afin de produire des angles couvrant les quatre quadrants.

Résumé
* La démodulation en quadrature peut extraire des informations d'angle pertinentes à la fois pour la modulation de fréquence et la modulation de phase.

* Les systèmes radio peuvent utiliser un processeur de signal numérique (en conjonction avec un convertisseur analogique-numérique) pour appliquer l'analyse mathématique aux formes d'onde I / Q.

* La phase en bande de base peut être obtenue en prenant l'arc tangente du rapport Q sur I; une fonction «atan2» est nécessaire si le système doit être capable de reproduire la totalité des 360 ° de phase.

* La fréquence de bande de base peut être obtenue en prenant la dérivée de l'arc tangente du rapport de Q à I.

Laisser un message 

Liste des messages